Detecting magnetic monopoles
References:
- Griffiths, David J. (2007), Introduction to Electrodynamics, 3rd Edition; Pearson Education – Problem 7 .36.
- Blas Cabrera (1982), Physical Review Letters, 48, 1378.
Although magnetic monopoles have never been found (at least,
reproducibly), one experiment that tried to find them was that of
Cabrera in 1982. The experiment was a fairly simple setup, consisting of
a superconducting (and therefore zero-resistance) wire loop with a
magnet aligned so that monopoles, should they exist, could pass through
the loop. Assuming that a single magnetic ‘charge’
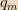 emits a magnetic field that obeys a Coulomb-like law, that is
emits a magnetic field that obeys a Coulomb-like law, that is
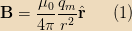
we can work out the magnetic flux through the loop as a single monopole falls through it.
If the speed of the monopole is
 and it falls along the axis of the loop then, assuming the loop has radius
and it falls along the axis of the loop then, assuming the loop has radius
 and we take as the area of integration the flat circle within the loop, we need to work out
and we take as the area of integration the flat circle within the loop, we need to work out
 to get the flux. Suppose the monopole is a distance
to get the flux. Suppose the monopole is a distance
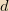 from the centre of the loop. Then the distance from the monopole to a point on the disk with radius
from the centre of the loop. Then the distance from the monopole to a point on the disk with radius
 is
is
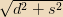 so the field strength at that point is
so the field strength at that point is
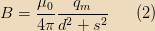
The term
 isolates the component of
isolates the component of
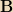 that is perpendicular to the disk, which is
that is perpendicular to the disk, which is
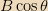 where
where
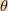 is the angle between the axis and a line from the monopole to a point on the disk at radius
is the angle between the axis and a line from the monopole to a point on the disk at radius
 . We get
. We get
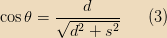
so the flux from the monopole is
 |
 |
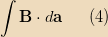 |
 |
 |
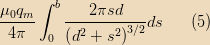 |
 |
 |
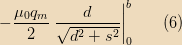 |
 |
 |
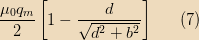 |
If we take
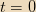 to be the time when the monopole crosses the plane of the disk and take
the surface normal at the disk to point in the direction of the
monopole’s velocity, then
to be the time when the monopole crosses the plane of the disk and take
the surface normal at the disk to point in the direction of the
monopole’s velocity, then
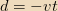 for
for
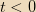 and
and
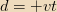 for
for
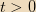 , and
, and
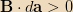 for
for
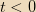 and
and
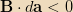 for
for
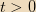 . That is
. That is
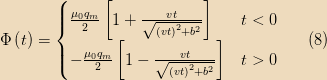
To go further, we need to modify Maxwell’s equations to include magnetic charge. The relevant one is Faraday’s law which needs an extra term:
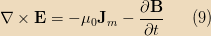
where
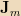 is the magnetic current density. This is the analog to the
is the magnetic current density. This is the analog to the
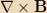 equation which involves electric current density. Applying Stokes’s
theorem, we can integrate the LHS around the loop and the RHS over the
disk enclosed:
equation which involves electric current density. Applying Stokes’s
theorem, we can integrate the LHS around the loop and the RHS over the
disk enclosed:
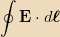 |
 |
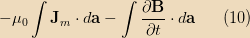 |
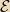 |
 |
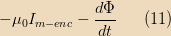 |
where
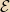 is the induced
back emf
and
is the induced
back emf
and
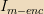 is the magnetic current flowing through the loop. This emf can be written in terms of the self-inductance
is the magnetic current flowing through the loop. This emf can be written in terms of the self-inductance
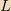 of the loop:
of the loop:
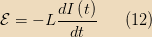
What are we to make of
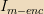 considering we have only a single monopole to make up the current? We can write it as a delta function:
considering we have only a single monopole to make up the current? We can write it as a delta function:
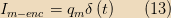
That is, there is a current consisting of a single charge across the disk only at time
 . Since the delta function is the
derivative of the step-function
. Since the delta function is the
derivative of the step-function
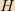 , we can integrate Faraday’s law to get
, we can integrate Faraday’s law to get
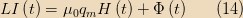
So we get
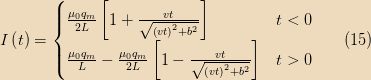
The
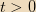 term comes out to be the same as the
term comes out to be the same as the
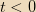 term, so we get in general
term, so we get in general
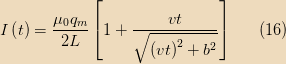
For
 ,
,
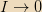 , while for
, while for
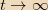 ,
,
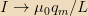 .
This means that, when the monopole is infinitely far away and
approaching, there is no induced current. The current increases as the
monopole gets closer, but since the superconducting loop has no
resistance, the current that is built up due to the back emf never
dissipates and tends to a constant non-zero value as the monopole
recedes into the distance.
.
This means that, when the monopole is infinitely far away and
approaching, there is no induced current. The current increases as the
monopole gets closer, but since the superconducting loop has no
resistance, the current that is built up due to the back emf never
dissipates and tends to a constant non-zero value as the monopole
recedes into the distance.
Related
- Magnetic monopole force law Mon, 18 November 2013 in "Electrodynamics"
- Magnetic dipoles versus monopoles; an experiment Tue, 9 July 2013 in "Electrodynamics"
- Fields of a moving magnetic monopole Sun, 22 February 2015 in "Electrodynamics"